PNG イメージを自力でパースしてみる ~1/6 予備知識編~
DirectX12でなにか作りたいと思って、じゃあとりあえず、まずはその辺のサンプルを読み漁ろうと、上のサイトさんからサンプルプログラムを拝借していろいろ見ていたとき、

"HelloTexture"
テクスチャを画面に表示させるサンプルを見つけて、たぶんここで画像ファイルをロードする機能とか、紹介してるんじゃないかな.. と思ってたのだけど、どうやら違った。
HelloTextureサンプルのテクスチャ元の画像ファイルが見つからない..?
— ロヴスタング=パシフィケイナス (@DarkCrowCorvus) 2016年6月4日
もしかしてソース内で動的に作ってる..?
代わりにテキトウなイメージを実行中に作っていた様子。画像ファイルをロードするためには、自身でそのまわり、なにかしらの準備をしないといけないみたい。
どこかのライブラリを拝借してきてもよかったものの、自身の勉強になるかと思い、じゃあ自作しましょうと、
自身が比較的よく使ってたフォーマットがPNGだから、じゃあPNGのパーサーを作ってみようかなと―――..
ということで、タイトルの通りに至る。
泥沼のはじまり
でふれーと圧縮とは。。。
— ロヴスタング=パシフィケイナス(@DarkCrowCorvus) 2016年6月19日
解説してるサイトさんとか探せばすぐに終わるかな...
なんて思ってたけど、そうも甘くなかった。 PNGが圧縮を使用していて..ということまでは知っていたものの 、実際にその正体が何でどんな圧縮方法なのかまでは知らない。
C++の標準で ”デフレート” なんて機能は提供されていない様子。後で調べたら linuxだとそれに相当するライブラリがデフォルトで使えるらしい、ただ自分のPCはwinだしなぁ..
ないなら作ればいいじゃない
いや...標準とか、デフォルトで提供されていないだけで、
google先生を使えば、そこらへんにライブラリが転がってたりはするのだけど...
中途半端に他人のライブラリを使いたくないだとかなんだとか...いつもの自前主義精神(?) がはたらいてしまって、結局自身で作ってみるに至る。
じゃあとりあえず ”デフレート” に関して調べてみる。よく見た回答は、wiki先生から言葉を拝借すると次の通り
Deflate(デフレート)とはLZ77とハフマン符号化を組み合わせた可逆データ圧縮アルゴリズム。
"可逆圧縮" なら知ってる、でもそのほかがよくわからない。"ハフマン符号化" は言葉だけ、どこかで聞いたことあるなぁ...ってレベル。
まずはその辺、調べてみるところから始めた。
調べたことを自分なりに整理して、以下に書き並べてみる。
以上。前置き終わり。
ハフマン符号化
データ圧縮アルゴリズムの一つ。
ハフマン符号化では、圧縮したいデータに含まれている各々の文字を、それぞれ別の ビット並び に置き換える、ということを行う
以降、この置き換えたビット並びのことを 符号 とよぶ。
この符号化のとき 元のデータの中で出現回数の多い文字にほど
短い符号を割り当てることで、全体的なデータサイズを減らそう
というのがハフマン符号化の基本的な圧縮の仕組み

同じ考え方の圧縮方法は、これ以外にもいくつかの種類があるのだけれど、ハフマン符号化はその中でも、符号化後のデータに含まれる符号の長さの平均が最小になるのだとか。
ハフマン符号化によって割り当てられた符号は、そのビット並びが、他のどの符号の頭の部分とも一致しないという特性を持つ。
この特性のことを 語頭条件 とよび、
語頭条件の特性を持つ符号は 接頭符号(Prefix code) とよばれる。
この通りに符号化することで、元のデータに戻すとき、その符号と同じビット並びが読み出せれば、それより後ろのビット並びに依存することなく、元の文字へ一意に復号することができるようになる。
この特性は 瞬時復号可能 と呼ばれる。

ハフマン符号は 接頭符号 であり、瞬時復号可能 な特性を持つ。
ただ単純に短い符号を割り当てればいい、っていうわけではないみたい。
カノニカル・ハフマン符号化(ハフマン符号の正規化)
ハフマン符号化でデータサイズを小さくできても、元の文字との対応がわからなければ、送った先でデータを復元することができない。
そのため圧縮したデータに、符号表を埋め込む必要があるのだけど、ここでの 符号 という存在が わりと厄介。
符号 はそれと対応する文字ごとに、長さの異なる ”可変長” なデータなのだけれど、データを復元する側では、各々の 符号 の情報を抽出するとき、何ビット分だけデータを読めばいいのか、わかっていないといけない。

パッと思いつく方法は 例えば上の通り、いっしょに 符号の長さ情報を持たせるなど。ただし、長さの情報を含むことによって、符号表全体のサイズが膨らんでしまう。
また、符号自体のサイズが大きくなりうる、というのも問題。
0x00 ~ 0xFF まで 256種類すべての文字に符号を割り当てる場合、一番長い符号は、最悪で255ビットにもなる(圧縮しないままの文字32コ分ぐらい)
※ここでは本来、アルファベットなどの文字として表すことのできない バイナリデータ中の8ビット並びも "文字" として扱うことにする。
そんなに大きな符号が生成されることはめったにないらしいのだけれど、万が一、そんな符号があると、符号表はその分だけ大きくなる、
符号表のサイズが膨らむと、それだけ全体のサイズも膨らんでしまうため、
符号化したら、前よりもデータサイズが増えたんだけど!?
なんてことが起こりうる。
こんなことじゃハフマン符号化を利用する意味がなくなってしまう。データの圧縮効果を上げるためには、この符号表をできる限り小さく保つ必要がある。
そこで カノニカル・ハフマン という手法を利用する。
これを利用すると、符号表のサイズを小さくするうえで悩みの種である 符号 を、
そのまま符号表の中に納めなくても済むようになる。
代わりに符号表には、各文字に対応する符号の 長さの情報だけ を納める。
カノニカル・ハフマン符号化 による 符号化の手順は以下の通り。
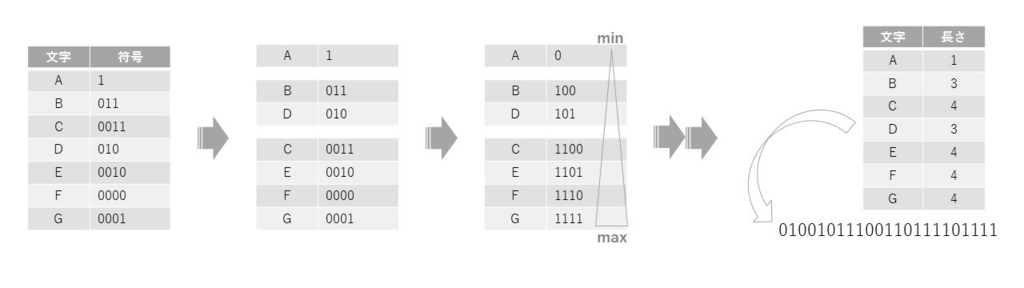
- 一度ふつうにハフマン符号化された符号を、
符号の長さ別 にグループ分けして、
そのグループ内で 文字番号の昇順 になるように並べる - 符号の長さが短く、文字番号の小さい文字ほど、
小さな符号になるように符号を割り当てなおす - 割り当てなおした符号表を使ってデータを符号化(圧縮)
- 符号の長さだけを納めた表を、符号化したデータの前に付加する
ポイントは、ある符号長グループへの 符号の再割り当てが終わって、次の符号長のグループに移るとき。
ひとつ前の符号長グループで一番最後に割り当てた符号に +1 したあと、その後ろに 0 ビットを付加したものを、次の符号長グループの再割り当てに利用する、ということ
この通りにすることで、再割り当てされた符号は 接頭符号 になり、瞬時復号可能な特性を持つようになる。

一方で、復号の手順は以下の通り。

- 符号の長さ表を読み出した後、
それを 符号の長さ別 にグループ分けして、
そのグループ内で 文字番号の昇順 になるように並べる - 符号の長さが短く、文字番号の小さい文字ほど、
小さな符号になるように符号を割り当て、符号表を復元する - 得られた符号表を使ってデータを復号する
LZ77符号化
データ圧縮アルゴリズムの一つ
Lempel さんと Ziv さんが 1977年に作ったからこんな名前
データ中の ある文字列が、それよりも以前に同じ形で現れているならば、文字列をその "位置" と "一致した長さ" という情報に置き換えてしまうことで、全体的なデータサイズを減らそう、というのが LZ77の大まかな圧縮の仕組み
"位置" と "一致した長さ" に置き換えるために、”以前に同じ形があるか” を検索できる範囲は有限で、直前に読みだせた文字から、何文字前まで...というのが事前に決められている。
これは 検索にかかる時間や 使用メモリ量、置換後の "位置" を表す数値が、巨大になり過ぎないように制限するため。
たとえばDeflateなら、直前に読み出した文字から、最大で 32,768文字前までが検索範囲。
新しい文字を読み出すたびに、検索できる範囲がスライドするため、この範囲のことを スライド窓(Sliding Window) と呼んだりする。
LZ77では、圧縮対象のデータを 先頭から順番に読み込み、
そのときに現れた文字、または文字列を
(位置 , 一致した長さ , 直近の不一致文字)
というフォーマットに置き換えることでデータの圧縮を行う。

圧縮元のデータが大きいほど、スライド窓の中に同じ文字列があるという機会が増えるため、圧縮効率が良くなるのだけれど、
上の例だと、対象のデータが短すぎるせいか、逆にサイズが増えてしまってる。
なんてこというと、ハフマン符号の時に提示した例も、圧縮後のデータに符号表を含めると、元のデータよりもサイズが大きくなってしまうのだけれど...
LZ77では何が何でも(位置, 一致した長さ, 直近の不一致文字)というフォーマットへ置き換えようとするため、スライド窓に同じ文字列が見つからなかった場合は、むしろ置換前よりもデータが大きくなってしまう という欠点がある。
LZ77には、それを基本形とするさまざまな亜種が存在する。
LZSS符号化
データ圧縮アルゴリズムでLZ77の亜種のうちの一つ。
StorerさんとSzymanskiさんが改良を行ったからこんな名前。
現在 普及している圧縮プログラムで LZ77 符号と呼ばれているもののほとんどは、じつは LZSS 符号になっている。とのこと ※1
実際、”LZ77を利用している” と言っていたDeflateも、その実装は、どちらかといえばLZSSのものに近い。
LZSS ではスライド窓の中を検索して、同じ文字列が存在し、さらに置換することで圧縮効果が得られる場合に限ってそれを "位置" と "一致した長さ" の情報に置き換る。それ以外の場合は置き換えを行わない。
この通りに作られた圧縮データは、復号のとき先頭から順番に読み出されたそれが "位置"と"一致した長さ" を表すのか、置換されなかった文字そのままを表すのかを判断できなければ、データを正しく復元することができない。
これの解決には、記録する各々の要素の先頭に 1ビットを付加する、という方法を用いる。
これによって 復号時には、各々の要素ごとに先頭の 1ビットを読んで、
それが "1" ならばその直後に続くデータは "位置" と "一致した長さ"
"0" ならば1文字そのまま..という具合に識別することができる。

識別のため、各々の要素に それぞれ 1ビットずつ付与されるため、"位置" と ”一致した長さ” の情報に 置換が行われなかった文字は、圧縮前よりも 1ビット分だけ大きくなるのだけれど、
それでもLZ77と比べると、スライド窓に同じ文字列が見つからなかったときにデータが膨らんでしまう規模を、だいぶん抑えることができる。
参考にしたサイトさん
全般
ハフマン符号
データ圧縮の基礎『ハフマン符号化』の仕組みを見てみよう - 道すがら講堂
圧縮アルゴリズム (3) ハフマン符号化 - 静的ハフマン圧縮
瞬時復号可能な符号 — Computer Science Textbook (under construction)
カノニカル・ハフマン符号化
圧縮アルゴリズム (4) ハフマン符号化 - 適応型ハフマン圧縮
Canonical Huffman code - Wikipedia, the free encyclopedia
LZ77
デフレート圧縮(LZ77圧縮)処理の概要 - ウェブで用いられる画像形式。
Data Compression/data differencing - Wikibooks, open books for an open world
LZSS